Distribusi Peluang Kontinu dan Cara Pembacaan Tabel-Tabel Distribusi

By Nand Syaputra - Januari 11, 2016

A. Pengertian Distribusi Peluang Kontinu
Distribusi peluang kontinu adalah peubah acak yang dapat memperoleh semua nilai pada skala kontinu. Ruang sampel kontinu adalah bila ruang sampel mengandung titik sampel yang tak terhingga banyaknya. Syarat dari distribusi kontinu adalah apabila fungsi f(x) adalah fungsi padat peluang peubah acak kontinu X yang didefinisikan di atas himpunan semua bilangan riil R bila:
1. F(x) ≥ 0 untuk semua x є R
2. ∫𝑓(𝑥)𝑑𝑥=1∞∞
3. 𝑃(𝑎<𝑋<𝑏)= ∫𝑓(𝑥)𝑑𝑥∞∞
B. Konsep dan Teorema Distribusi
1. Distribusi Normal
Distribusi normal merupakan suatu alat statistik yang sangat penting untuk menaksir dan meramalkan peristiwa-peristiwa yang lebih luas. Distribusi normal disebut juga dengan distribusi Gauss untuk menghormati Gauss sebagai penemu persamaannya (1777-1855). Menurut pandangan ahli statistik, distribusi variabel pada populasi mengikuti distribusi normal. 
Distribusi normal pertama kali diperkenalkan oleh Abraham DeMoivre (1733) sebagai pendekatan distribusi binomial untuk n besar. Selanjutnya dikembangkan oleh Pierre Simon de Laplace dan dikenal dengan Teorema Moivre - Laplace. Laplace menggunakan distribusi normal untuk analisis galat suatu eksperimen. 

Suatu data membentuk distribusi normal jika jumlah data di atas dan di bawah mean adalah sama. Distribusi normal berupa kurva berbentuk lonceng setangkup yang melebar tak berhingga pada kedua arah positif dan negatifnya.
Ciri-ciri kurva normal :
  1. Bentuk kurva normal
    1. Menyerupai lonceng (genta/bel).
    2. Merupakan suatu poligon yang dilicinkan yang mana ordinat (sumbu tegak) merupakan frekuensi dan absisnya (sumbu alas) memuat nilai variabel.
    3. Simetris.
    4. Luas daerah merupakan nilai rata-rata (mean).
    5. Luas daerah sebelah kiri dan kanan mendekati 50%.
    6. Memiliki satu modus (disebut juga bimodal).
  2. Daerah kurva normal
    1. Merupakan ruangan yang dibatasi daerah kurva dengan absisnya (sumbu alas).
    2. Luas daerah biasanya dinyatakan dalam persen atau proporsi.


Distribusi normal dipengaruhi oleh dua parameter, yaitu mean dan standar deviasi.
Mean menentukan lokasi pusat statistik dan standar deviasi menentukan lebar dari kurva normal.

Rumus umum distribusi normal :


dengan 

Kurva normal menggambarkan daerah penerimaan dan penolakan Ho. 

 Jika pengujian dua arah / sisi, maka gambarnya sebagai berikut :


Jika pengujian satu arah, maka gambarnya sebagai berikut :

 

Uji satu arah biasanya untuk uji F dan uji t satu arah.

2. Distribusi Chi Kuadrat (χ2)
Apa itu chi square? Chi Square merupakan salah jenis uji hipotesa yang dikenal dalam statistik. Distribusi chi square dilambangkan dengan χ2. Kegunaan Uji Chi Square adalah untuk menguji hubungan ataupengaruh dua buah variabel nominal dan mengukur kuatnya hubungan antara variabel yang satu dengan variabel nominal lainnya (C = Coefisien of contingency).
Karakteristik Chi‐Square:
  • Nilai Chi‐Square selalu positip.
  • Terdapat beberapa keluarga distribusi Chi‐Square, yaitu distribusi Chi‐Square dengan DK=1, 2, 3, dst.
  • Bentuk Distribusi Chi‐Square adalah menjulur positip.Semakin besar derajat bebas, semakin mendekati distribusi normal.
  • df = k – 1, dimana k adalah jumlah katagori. Jadi bentuk distribusi chi square tidak ditentukan banyaknya sampel, melainkan banyaknya derajat bebas.
Rumus Chi Square
χ2: Nilai chi-kuadrat
fe: Frekuensi yang diharapkan
fo: Frekuensi yang diperoleh/diamati

3. Distribusi F

Menurut Gasperz (1989:251), secara teori sebaran F merupakan rasio dari dua sebaran chi kuadrat yang bebas. Oleh karena itu peubah acak F diberikan sebagai: 𝐹=𝑋12𝑉1⁄𝑋22𝑉2⁄
Dimana : 𝑋12= 𝑛𝑖𝑙𝑎𝑖 𝑑𝑎𝑟𝑖 𝑠𝑒𝑏𝑎𝑟𝑎𝑛 𝑐ℎ𝑖 𝑘𝑢𝑎𝑑𝑟𝑎𝑡 𝑑𝑒𝑛𝑔𝑎𝑛 𝑑𝑒𝑟𝑎𝑗𝑎𝑡 𝑏𝑒𝑏𝑎𝑠 𝑉1=𝑛1−1 𝑋22= 𝑛𝑖𝑙𝑎𝑖 𝑑𝑎𝑟𝑖 𝑠𝑒𝑏𝑎𝑟𝑎𝑛 𝑐ℎ𝑖 𝑘𝑢𝑎𝑑𝑟𝑎𝑡 𝑑𝑒𝑛𝑔𝑎𝑛 𝑑𝑒𝑟𝑎𝑗𝑎𝑡 𝑏𝑒𝑏𝑎𝑠 𝑉2=𝑛2−1
Oleh karena itu sebaran F mempunyai dua derajat bebas yaitu 𝑉1 𝑑𝑎𝑛 𝑉2.
Misal :
Kita ingin mengetahui nilai F dengan derajat bebas 𝑉1=10

CARA PEMBACAAN TABEL-TABEL Z, T, χ2, dan F
Tabel Distribusi Z
tabel z dari 0 sampai 4 dan tabel z dari -4 sampai nol (langsung gabung dalam bentuk html)
z00,010,020,030,040,050,060,070,080,09
0,00,500000,503990,507980,511970,515950,519940,523920,527900,531880,53586
0,10,539830,543800,547760,551720,555670,559620,563560,567490,571420,57535
0,20,579260,583170,587060,590950,594830,598710,602570,606420,610260,61409
0,30,617910,621720,625520,629300,633070,636830,640580,644310,648030,65173
0,40,655420,659100,662760,666400,670030,673640,677240,680820,684390,68793
0,50,691460,694970,698470,701940,705400,708840,712260,715660,719040,72240
0,60,725750,729070,732370,735650,738910,742150,745370,748570,751750,75490
0,70,758040,761150,764240,767300,770350,773370,776370,779350,782300,78524
0,80,788140,791030,793890,796730,799550,802340,805110,807850,810570,81327
0,90,815940,818590,821210,823810,826390,828940,831470,833980,836460,83891
1,00,841340,843750,846140,848490,850830,853140,855430,857690,859930,86214
1,10,864330,866500,868640,870760,872860,874930,876980,879000,881000,88298
1,20,884930,886860,888770,890650,892510,894350,896170,897960,899730,90147
1,30,903200,904900,906580,908240,909880,911490,913080,914660,916210,91774
1,40,919240,920730,922200,923640,925070,926470,927850,929220,930560,93189
1,50,933190,934480,935740,936990,938220,939430,940620,941790,942950,94408
1,60,945200,946300,947380,948450,949500,950530,951540,952540,953520,95449
1,70,955430,956370,957280,958180,959070,959940,960800,961640,962460,96327
1,80,964070,964850,965620,966380,967120,967840,968560,969260,969950,97062
1,90,971280,971930,972570,973200,973810,974410,975000,975580,976150,97670
2,00,977250,977780,978310,978820,979320,979820,980300,980770,981240,98169
2,10,982140,982570,983000,983410,983820,984220,984610,985000,985370,98574
2,20,986100,986450,986790,987130,987450,987780,988090,988400,988700,98899
2,30,989280,989560,989830,990100,990360,990610,990860,991110,991340,99158
2,40,991800,992020,992240,992450,992660,992860,993050,993240,993430,99361
2,50,993790,993960,994130,994300,994460,994610,994770,994920,995060,99520
2,60,995340,995470,995600,995730,995850,995980,996090,996210,996320,99643
2,70,996530,996640,996740,996830,996930,997020,997110,997200,997280,99736
2,80,997440,997520,997600,997670,997740,997810,997880,997950,998010,99807
2,90,998130,998190,998250,998310,998360,998410,998460,998510,998560,99861
3,00,998650,998690,998740,998780,998820,998860,998890,998930,998960,99900
3,10,999030,999060,999100,999130,999160,999180,999210,999240,999260,99929
3,20,999310,999340,999360,999380,999400,999420,999440,999460,999480,99950
3,30,999520,999530,999550,999570,999580,999600,999610,999620,999640,99965
3,40,999660,999680,999690,999700,999710,999720,999730,999740,999750,99976
3,50,999770,999780,999780,999790,999800,999810,999810,999820,999830,99983
3,60,999840,999850,999850,999860,999860,999870,999870,999880,999880,99989
3,70,999890,999900,999900,999900,999910,999910,999920,999920,999920,99992
3,80,999930,999930,999930,999940,999940,999940,999940,999950,999950,99995
3,90,999950,999950,999960,999960,999960,999960,999960,999960,999970,99997
4,00,999970,999970,999970,999970,999970,999970,999980,999980,999980,99998
Cara Menggunakan Tabel Z
Tabel Z sebenarnya digunakan untuk memudahkan sobat dalam menghitung peluang (kerapatan probablitas) dari  distribusi normal. Rumus fungsi kerapatan probabilitas dari distribusi normal adalah
rumus fungsi distribus normal (tabel z)Dimana μ adalah rata-rata, σ adalah standar deviasi dan π = 3,14159. Grafik fungsi distribusi normalnya sendiri seperti di bawah ini
tabel z or z table
Grafik fungsi distribusi normal tersebut di atas membentang dari minus tak hingga hingga tak hingga. Hanya saja, semakin jauh dengan rata-rata (M1), nilai probabilitas akan semakin mendekati nol. Mungkin kalau sobat hanya menghitung nilai probabilitas dari suatu angka/titik mungkin ngga begitu susah, tinggal dimasukkan ke rumus (susah juga sih)
rumus fungsi distribus normal (tabel z)Nah susahnya sobat, misal sobat menghitung probabilitas dari suatu range. Misal saja kita pakai contoh soal distribusi normal berikut
Rata-rata produktivitas padi di Aceh tahun 2009 adalah 6 ton per ha, dengan simpangan baku (s) 0,9 ton.  Jika luas sawah di Aceh 100.000 ha dan produktivitas padi berdistribusi normal (data tentatif), tentukan. Berapa luas sawah yang produktivitasnya lebih dari 8  ton? Sobat bisa saja ko pakai rumus berikut
menghitung probabilitasSuper njlimet kan kalau harus ngitung integral kaya gitu. Disinilah gunanya tabel Z. Kita hitung dulu nilai z dari soal di atas dengan rumus
Setelah itu tinggal kita gunakan tabel Z untuk menentukan probabilitasnya. Cara menggunakan tabel Z nya sebagai berikut
  1. Caranya buka Tabel Z dan lihat  sel pada perpotongan baris 2,20 dan kolom 0,02.
  2.  Sobat akan menemukan sebuah angka yaitu 0,98679 dan bila dijadikan persen menjadi 98,679%.
  3. Angka yang sobat temukan di tabel z tersebut menunjukkan  luas di bawah kurva normal baku dari titik 2,22 ke kiri kurva yaitu 98,679%. Karena luas seluruh di bawah kurva normal adalah 100%, maka luas dari titik 2,22 ke kanan kurva adalah 100% – 98,679% = 1,321% (arsir warna hitam pada gambar).  Oleh karena itu, luas sawah yang produktivitasnya lebih dari 8 ton adalah 1,321%, yaitu (1,321/100) x 100.000 ha = 1321 ha. Mudah kan sobat kalau pakai tabel Z. :D

Tabel Distribusi T

d.f.
TINGKAT SIGNIFIKANSI
dua sisi
20%
10%
5%
2%
1%
0,2%
0,1%
satu sisi
10%
5%
2,5%
1%
0,5%
0,1%
0,05%
1
3,078
6,314
12,706
31,821
63,657
318,309
636,619
2
1,886
2,920
4,303
6,965
9,925
22,327
31,599
3
1,638
2,353
3,182
4,541
5,841
10,215
12,924
4
1,533
2,132
2,776
3,747
4,604
7,173
8,610
5
1,476
2,015
2,571
3,365
4,032
5,893
6,869
6
1,440
1,943
2,447
3,143
3,707
5,208
5,959
7
1,415
1,895
2,365
2,998
3,499
4,785
5,408
8
1,397
1,860
2,306
2,896
3,355
4,501
5,041
9
1,383
1,833
2,262
2,821
3,250
4,297
4,781
10
1,372
1,812
2,228
2,764
3,169
4,144
4,587
11
1,363
1,796
2,201
2,718
3,106
4,025
4,437
12
1,356
1,782
2,179
2,681
3,055
3,930
4,318
13
1,350
1,771
2,160
2,650
3,012
3,852
4,221
14
1,345
1,761
2,145
2,624
2,977
3,787
4,140
15
1,341
1,753
2,131
2,602
2,947
3,733
4,073
16
1,337
1,746
2,120
2,583
2,921
3,686
4,015
17
1,333
1,740
2,110
2,567
2,898
3,646
3,965
18
1,330
1,734
2,101
2,552
2,878
3,610
3,922
19
1,328
1,729
2,093
2,539
2,861
3,579
3,883
20
1,325
1,725
2,086
2,528
2,845
3,552
3,850
21
1,323
1,721
2,080
2,518
2,831
3,527
3,819
22
1,321
1,717
2,074
2,508
2,819
3,505
3,792
23
1,319
1,714
2,069
2,500
2,807
3,485
3,768
24
1,318
1,711
2,064
2,492
2,797
3,467
3,745
25
1,316
1,708
2,060
2,485
2,787
3,450
3,725
26
1,315
1,706
2,056
2,479
2,779
3,435
3,707
27
1,314
1,703
2,052
2,473
2,771
3,421
3,690
28
1,313
1,701
2,048
2,467
2,763
3,408
3,674
29
1,311
1,699
2,045
2,462
2,756
3,396
3,659
30
1,310
1,697
2,042
2,457
2,750
3,385
3,646
31
1,309
1,696
2,040
2,453
2,744
3,375
3,633
32
1,309
1,694
2,037
2,449
2,738
3,365
3,622
33
1,308
1,692
2,035
2,445
2,733
3,356
3,611
34
1,307
1,691
2,032
2,441
2,728
3,348
3,601
35
1,306
1,690
2,030
2,438
2,724
3,340
3,591
36
1,306
1,688
2,028
2,434
2,719
3,333
3,582
37
1,305
1,687
2,026
2,431
2,715
3,326
3,574
38
1,304
1,686
2,024
2,429
2,712
3,319
3,566
39
1,304
1,685
2,023
2,426
2,708
3,313
3,558
40
1,303
1,684
2,021
2,423
2,704
3,307
3,551
41
1,303
1,683
2,020
2,421
2,701
3,301
3,544
42
1,302
1,682
2,018
2,418
2,698
3,296
3,538
43
1,302
1,681
2,017
2,416
2,695
3,291
3,532
44
1,301
1,680
2,015
2,414
2,692
3,286
3,526
45
1,301
1,679
2,014
2,412
2,690
3,281
3,520
46
1,300
1,679
2,013
2,410
2,687
3,277
3,515
47
1,300
1,678
2,012
2,408
2,685
3,273
3,510
48
1,299
1,677
2,011
2,407
2,682
3,269
3,505
49
1,299
1,677
2,010
2,405
2,680
3,265
3,500
50
1,299
1,676
2,009
2,403
2,678
3,261
3,496
51
1,298
1,675
2,008
2,402
2,676
3,258
3,492
52
1,298
1,675
2,007
2,400
2,674
3,255
3,488
53
1,298
1,674
2,006
2,399
2,672
3,251
3,484
54
1,297
1,674
2,005
2,397
2,670
3,248
3,480
55
1,297
1,673
2,004
2,396
2,668
3,245
3,476
56
1,297
1,673
2,003
2,395
2,667
3,242
3,473
57
1,297
1,672
2,002
2,394
2,665
3,239
3,470
58
1,296
1,672
2,002
2,392
2,663
3,237
3,466
59
1,296
1,671
2,001
2,391
2,662
3,234
3,463
60
1,296
1,671
2,000
2,390
2,660
3,232
3,460
61
1,296
1,670
2,000
2,389
2,659
3,229
3,457
62
1,295
1,670
1,999
2,388
2,657
3,227
3,454
63
1,295
1,669
1,998
2,387
2,656
3,225
3,452
64
1,295
1,669
1,998
2,386
2,655
3,223
3,449
65
1,295
1,669
1,997
2,385
2,654
3,220
3,447
66
1,295
1,668
1,997
2,384
2,652
3,218
3,444
67
1,294
1,668
1,996
2,383
2,651
3,216
3,442
68
1,294
1,668
1,995
2,382
2,650
3,214
3,439
69
1,294
1,667
1,995
2,382
2,649
3,213
3,437
70
1,294
1,667
1,994
2,381
2,648
3,211
3,435
71
1,294
1,667
1,994
2,380
2,647
3,209
3,433
72
1,293
1,666
1,993
2,379
2,646
3,207
3,431
73
1,293
1,666
1,993
2,379
2,645
3,206
3,429
74
1,293
1,666
1,993
2,378
2,644
3,204
3,427
75
1,293
1,665
1,992
2,377
2,643
3,202
3,425
76
1,293
1,665
1,992
2,376
2,642
3,201
3,423
77
1,293
1,665
1,991
2,376
2,641
3,199
3,421
78
1,292
1,665
1,991
2,375
2,640
3,198
3,420
79
1,292
1,664
1,990
2,374
2,640
3,197
3,418
80
1,292
1,664
1,990
2,374
2,639
3,195
3,416
81
1,292
1,664
1,990
2,373
2,638
3,194
3,415
82
1,292
1,664
1,989
2,373
2,637
3,193
3,413
83
1,292
1,663
1,989
2,372
2,636
3,191
3,412
84
1,292
1,663
1,989
2,372
2,636
3,190
3,410
85
1,292
1,663
1,988
2,371
2,635
3,189
3,409
86
1,291
1,663
1,988
2,370
2,634
3,188
3,407
87
1,291
1,663
1,988
2,370
2,634
3,187
3,406
88
1,291
1,662
1,987
2,369
2,633
3,185
3,405
89
1,291
1,662
1,987
2,369
2,632
3,184
3,403
90
1,291
1,662
1,987
2,368
2,632
3,183
3,402
91
1,291
1,662
1,986
2,368
2,631
3,182
3,401
92
1,291
1,662
1,986
2,368
2,630
3,181
3,399
93
1,291
1,661
1,986
2,367
2,630
3,180
3,398
94
1,291
1,661
1,986
2,367
2,629
3,179
3,397
95
1,291
1,661
1,985
2,366
2,629
3,178
3,396
96
1,290
1,661
1,985
2,366
2,628
3,177
3,395
97
1,290
1,661
1,985
2,365
2,627
3,176
3,394
98
1,290
1,661
1,984
2,365
2,627
3,175
3,393
99
1,290
1,660
1,984
2,365
2,626
3,175
3,392
100
1,290
1,660
1,984
2,364
2,626
3,174
3,390

Kita lihat dulu bagian-bagian dari tabel T masing-masing kolom mulai dari kolom kedua (angka yang dicetak tebal) dari tabel tersebut adalah nilai probabilita atau tingkat signifikansi. Nilai yang lebih kecil menunjukkan probabilita satu arah (satu sisi) sedangkan nilai yang lebih besar menunjukkan probabilita kedua arah (dua sisi). Misalnya pada kolom kedua, angka 0,25 adalah probabilita satu arah sedangkan 0,50 adalah probabilita dua arah. Lanjut di bagian kiri ada degree of freedom (derajat kebebasan) seinget saya waktu kuliah dulu angkanya 1 sampai 200
Probabilita Pada Tabel T
Sebelum melakukan pengujian hipotesis terlebih dahulu kita tetapka apa yang disebut dengan probabilita. Probabilita itu adalah taraf signifikansi atau sering disebut alpha α.
Probabilita 1 arah dan probabilita 2 arah
Jenis probabilita tergantung pada rumusan hipotesis yang akan kita uji. Misal kita ingin menguji suatu hipotesis ” Dari sisi ini, pengujian hipotesis memiliki dua bentuk pengujian yaitu pengujian satu arah dan pengujian dua arah. Pengujian satu arah atau dua arah tergantung pada perumusan hipotesis yang akan kita uji. Misalnya jika hipotesis kita berbunyi, “ pendidikan berpengaruh positif terhadap pendapatan”. Artinya semakin tinggi pendidikan semakin besar pendapatan”. Maka pengujiannya menggunakan uji satu arah. Atau, misalnya “ umur berpengaruh negatif terhadap pendapatan”. Artinya semakin tua umur semakin rendah pendapatan”. Ini juga menggunakan pengujian satu arah.
Tetapi jika hipotesisnya berbunyi, “ terdapat pengaruh umur terhadap pendapatan”. Artinya umur bisa berpengaruh positif , tetapi juga bisa berpengaruh negatif terhadap pendapatan. Maka, pengujiannya menggunakan uji dua arah.
Kalau kita melakukan pengujian satu arah. Maka pada tabel t, lihat pada judul kolom bagian paling atasnya (angka yang kecilnya). Sebaliknya kalau kita  melakukan pengujian dua arah, lihat pada judul kolom angka yang besarnya.
Selanjutnya bagaimana menentukan  derajat bebas atau degree of freedom (df) tersebut ?
Dalam pengujian hipotesis untuk model regresi, derajat bebas ditentukan dengan rumus n – k. Dimana n = banyak observasi sedangkan k = banyaknya variabel (bebas dan terikat). (Catatan: untuk pengujian lain misalnya uji hipotesis rata-rata dllnya rumus ini bisa berbeda).
Tabel Distribusi Chi Kuadrat (χ2)
Berikut ini tabel Chi-Square dengan derajat kebebasan dari 1-100 dan alpha 0,001, 0,01, dan 0,05
dfP = 0.05P = 0.01P = 0.001dfP = 0.05P = 0.01P = 0.001
13.846.6410.835168.6777.3987.97
25.999.2113.825269.8378.6289.27
37.8211.3516.275370.9979.8490.57
49.4913.2818.475472.1581.0791.88
511.0715.0920.525573.3182.2993.17
612.5916.8122.465674.4783.5294.47
714.0718.4824.325775.6284.7395.75
815.5120.0926.135876.7885.9597.03
916.9221.6727.885977.9387.1798.34
1018.3123.2129.596079.0888.3899.62
1119.6824.7331.266180.2389.59100.88
1221.0326.2232.916281.3890.80102.15
1322.3627.6934.536382.5392.01103.46
1423.6929.1436.126483.6893.22104.72
1525.0030.5837.706584.8294.42105.97
1626.3032.0039.256685.9795.63107.26
1727.5933.4140.796787.1196.83108.54
1828.8734.8142.316888.2598.03109.79
1930.1436.1943.826989.3999.23111.06
2031.4137.5745.327090.53100.42112.31
2132.6738.9346.807191.67101.62113.56
2233.9240.2948.277292.81102.82114.84
2335.1741.6449.737393.95104.01116.08
2436.4242.9851.187495.08105.20117.35
2537.6544.3152.627596.22106.39118.60
2638.8945.6454.057697.35107.58119.85
2740.1146.9655.487798.49108.77121.11
2841.3448.2856.897899.62109.96122.36
2942.5649.5958.3079100.75111.15123.60
3043.7750.8959.7080101.88112.33124.84
3144.9952.1961.1081103.01113.51126.09
3246.1953.4962.4982104.14114.70127.33
3347.4054.7863.8783105.27115.88128.57
3448.6056.0665.2584106.40117.06129.80
3549.8057.3466.6285107.52118.24131.04
3651.0058.6267.9986108.65119.41132.28
3752.1959.8969.3587109.77120.59133.51
3853.3861.1670.7188110.90121.77134.74
3954.5762.4372.0689112.02122.94135.96
4055.7663.6973.4190113.15124.12137.19
4156.9464.9574.7591114.27125.29138.45
4258.1266.2176.0992115.39126.46139.66
4359.3067.4677.4293116.51127.63140.90
4460.4868.7178.7594117.63128.80142.12
4561.6669.9680.0895118.75129.97143.32
4662.8371.2081.4096119.87131.14144.55
4764.0072.4482.7297120.99132.31145.78
4865.1773.6884.0398122.11133.47146.99
4966.3474.9285.3599123.23134.64148.21
5067.5176.1586.66100124.34135.81149.48
Cara Membaca Tabel Chi-Square

Sama seperti dalam tabel T, dalam tabel ci-square ada yang namannya tingkata signifikasi (α ) serta derajad kebebasan (dk) atau degree of freedom. Tingkat signifikansi merupakan ukuran seberapa besar keyakinan yang kita ambil. Misalnya jika nilai α (alpha) adalah 0,01 maka kita memiliki keyakinan bahwa keputusan yang kita ambil 90% benar. Derajat kebebasan didapat dengan rumus n-1. Jadi jika kita memiliki n observasi maka derajad bebasnya adalah n-1. Jika obyek yang kita teliti berjumlah 60 maka derajad bebasnya adalah 60-1 = 59.

Tabel Distribusi F 
Salah satu bentuk struktur tabel F yang tersedia adalah sebagai berikut: 
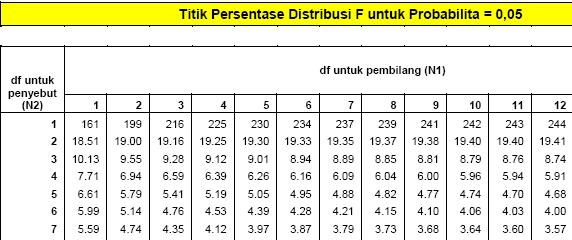
Judul tabel biasanya memuat keterangan mengenai nilai probabilita dari tabel F yang disajikan. Dalam contoh diatas, probabilitanya adalah 0,05. 
Lalu apa itu yang dimaksud dengan probabilita pada tabel F tersebut ? 
Dalam pengujian hipotesis, kita terlebih dahulu menetapkan tingkat/taraf signifikansi pengujian kita (biasanya disimbolkan dengan α (alpha)). Misalnya 1 %, 5 %, 10 % dan seterusnya. Nah, taraf/tingkat signifikansi tersebut yang merupakan probabilita dalam tabel ini. 
Judul masing-masing kolom mulai dari kolom kedua (angka yang dicetak tebal) dari tabel tersebut adalah derajat bebas/degree of freedom (df) untuk pembilang, atau dikenal dengan df1. Juga sering disimbolkan dalam tabel F dengan simbol N1 seperti tabel diatas. 
Selanjutnya, judul masing-masing baris adalah derajat bebas/degree of freedom (df) untuk penyebut, atau dikenal dengan df2. Juga sering disimbolkan dalam tabel F dengan simbol N2 seperti tabel diatas. 
Bagaimana menentukan df1 (N1) dan df2 (N2) tersebut ? 
Rumusnya:
df1 = k -1 df2 = n – k 
dimana k adalah jumlah variabel (bebas + terikat) dan n adalah jumlah observasi/sampel pembentuk regresi. 
Misalnya kita punya persamaan regresi dengan dua variabel bebas dan satu variabel terikat. Jumlah sampel pembentuk regresi tersebut sebanyak 10. Maka df1= k-1 = 3 – 1 = 2 sedangkan df2 = n – k = 10 – 3 = 7 
Jika pengujian dilakukan pada α = 5%, maka nilai F tabelnya adalah 4,74. Lihat pada N1=2 dan N2= 7 pada tabel diatas. 
Sebagai catatan, juga terdapat format tampilan tabel F seperti gambar dibawah ini. Pada prinsipnya sama, yang membedakan adalah, probabilitanya di letakkan dalam satu kolom setelah N2. Dengan demikian jika kita ingin mencari nilai F tabel misalnya dengan df1=2, df2 = 2 dan α = 5%, maka lihat pada N1= 2, N2 =2 pada baris 0.05

Sumber :
http://jam-analyst.blogspot.co.id/2012/02/distribusi-normal.html
http://rumushitung.com/2013/02/02/tabel-chi-square-dan-cara-menggunakannya/
http://www.portal-statistik.com/2015/05/cara-membaca-atau-melihat-tabel-t.html
http://rumushitung.com/2013/01/21/tabel-z-distribusi-normal/

  • Share:

You Might Also Like

0 komentar